【Rによるデータサイエンス】非線形回帰分析　〜　一般化線形モデル

一般化線形モデルとは・・・。
wikipediaから引用したものが次。

一般化線形モデル (いっぱんかせんけいモデル、英:Generalized linear model、GLM)は、正規分布以外の分布を扱えるように線形回帰モデルを拡張したモデル。

なるほど！たしかに、これまで「【Rによるデータサイエンス】線形回帰分析　〜　線形単回帰分析」や「【Rによるデータサイエンス】線形回帰分析　〜　重回帰分析」で扱った線形回帰分析では、残差は正規分布に従うと仮定していた。しかし、データが常に正規分布に従う保証はない。

一般化線形モデルでは、正規分布を拡張した分布族に対応させ、非線形の現象を線形モデルの場合と同じく簡単に扱え、かつ不自然な尺度で解釈しないように工夫したデータ解析の方法である。

線形モデルは $Y=AX+E$ で表される。一般化線形モデルでは、非線形関数を $g(\mu)=XA$ に変換して線形モデルとして扱う。ここで、 $\mu$ は目的変数の平均であり、gはリンク関数である。

◎ケーススタディ
さて、以前、「【Rによるデータサイエンス】線形回帰分析　〜　重回帰分析」で扱ったデータセットairqualityの残差の正規性分析の結果を思い出そう。
Ozoneを目的変数、Solar.RとWindとTempを説明変数とした線形回帰分析の残差の正規性は次のようにして可視化できる。
qqnormは、引数に対する、期待正規ランクスコアをプロットする。qqlineではqqnormにて書かれた上にデータの上四分位点と下四分位点を結ぶ直線を描く。

> air.lm<-lm(Ozone~ Solar.R+Wind+Temp,data=airquality) #線形回帰分析
> qqnorm(resid(air.lm)) 
> qqline(resid(air.lm),lwd=2,col="red")

緑のまるで囲ったように両端では直線から乖離しており、残差が正規分布に従うとは言いがたい。

そこで、残差が正規分布とガンマ分布の2つの場合について、一般化線形モデルを作成してみる。

> air.glm1<-glm(Ozone~Solar.R+Wind+Temp,data=airquality,family=gaussian)
> air.glm2<-glm(Ozone~Solar.R+Wind+Temp,data=airquality,family=Gamma)

AICを計算する。

> AIC(air.lm)
[1] 998.7171
> AIC(air.glm1)
[1] 998.7171
> AIC(air.glm2)
[1] 939.8778

AICの計算値を見ると、残差がガンマ分布に従うと仮定した一般化線形モデルが最も精度がよい。
qqnorm関数を使用してair.glm2に対する期待正規ランクスコアをプロットし、qqline関数を使用して上四分位点と下四分位点を結ぶ直線を描く。

> qqnorm(resid(air.glm2))
> qqline(resid(air.glm2),lwd=2,col="red")

次に、一般化線形モデルの関数glmによるロジスティック回帰を実施してみる。
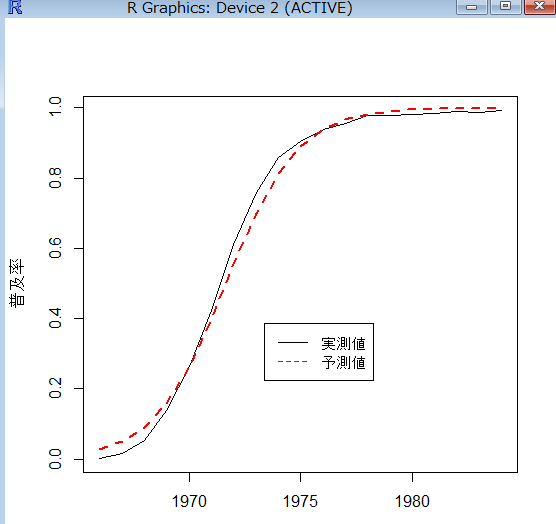
使用するデータは、以前使用したTVの使用率と年度のデータ。

> TV<-data.frame(年度,普及率)
> plot(TV)

これを関数glmによって一般化線形モデルに置き換えて、結果を可視化する。

> fm5<-glm(普及率~年度,data=TV,family=binomial)
> plot(年度,普及率,type="l")
> lines(年度,fitted(fm5),lty=2,col="red",lwd=2)
> legend(locator(1),c("実測値","予測値"),col=1:2,lty=1:2)

ここで理論的な背景を整理する。
そもそもロジスティック解析は、観測値x、観測値によって決まる値がp(x)があった時、関数pをロジスティック関数を使用して回帰分析することだった。そして、ロジスティック関数は線形ではなく非線形関数である。
ところが、関数glmによる一般化線形モデルによる回帰分析では、いつの間にか線形モデルに置き換えられている。それはどういうことか。

関数gを次のように定義する。